研究员 博士生导师
职务:统计系副主任
在职信息:在职
主要任职:黄山学者特聘教授
1、网络理论在复杂系统、通信网络的应用。相关成果发表在《SIAM Journal on Applied Dynamical Systems》,《Linear Algebra and its Applications》,《Chaos》等国际重要期刊上。代表性成果:
(1)原创性地提出了网络的 [t,p]-chain 分解方法,并用于研究网络上的传播动力学;并给出首个仅利用局部信息、分布式计算搜索网络里长路径的非平凡算法;
(2)揭示了任何偏序集的莫比乌斯函数可以通过构造一个线性网络系统部分状态更新计算得到。
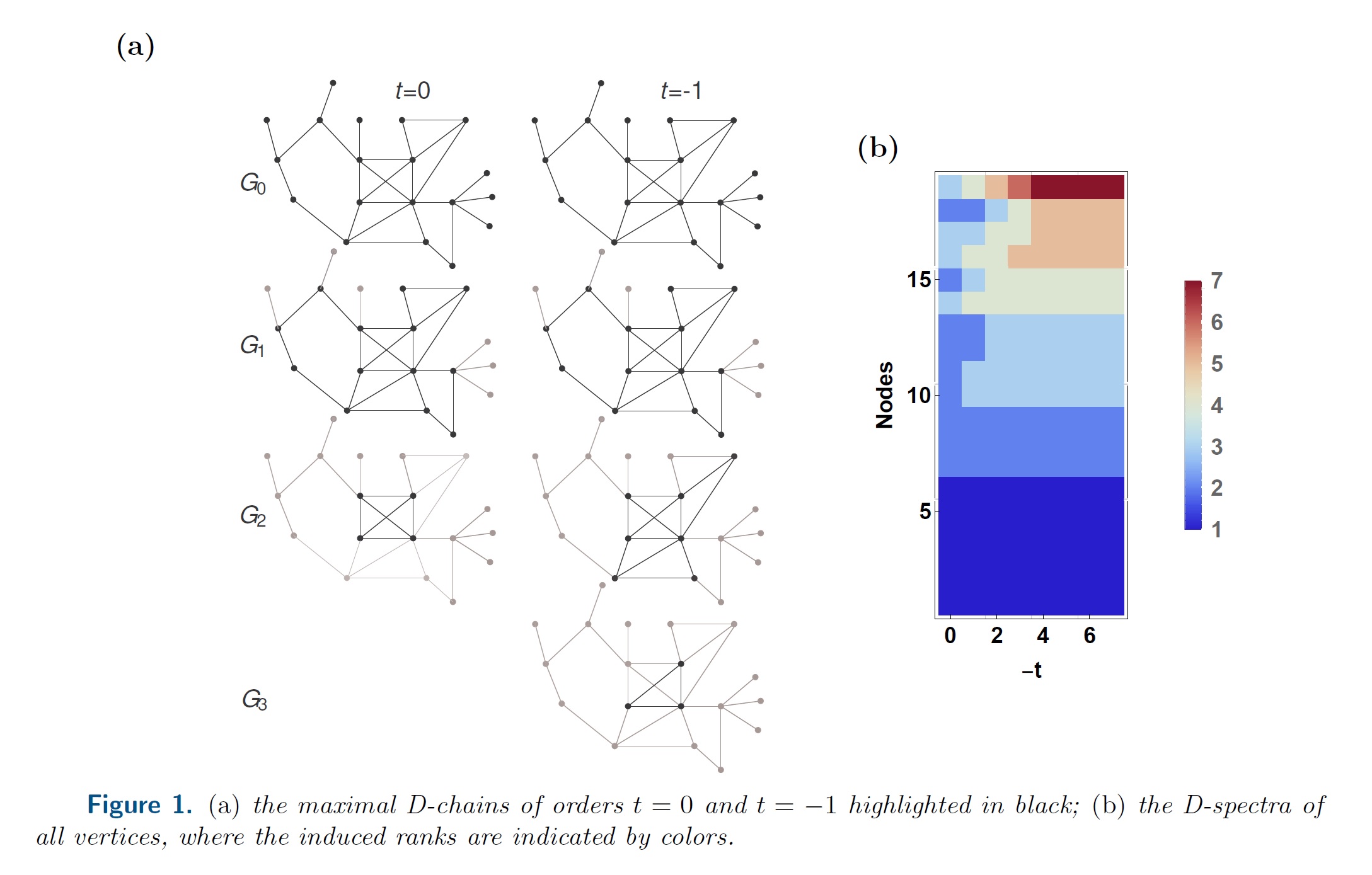
利用局部信息、分布式计算搜索网络里长路径
很多朋友都知道小世界理论或者六度分离理论,简单来讲,就是任何两个人可以通过少量的中间人建立关系。我们再回顾一下哈佛大学的社会学家斯坦利•米尔格拉姆(Stanley Milgram)的一个实验。他在内布拉斯卡州的奥马哈市随机挑选了大约 300 人,并给他们各自一封信,然后以这些人各自为起点,通过人传人转接的方式把手上的信交给一个波士顿的股票经纪人,在转接过程中,每个当前拿到信的人都把信交给一个他认识的、且他认为能更快将信送达给股票经纪人的人。实验结束,米尔格拉姆教授通过统计发现每个人大约只需要5个人中转就能将信送达。
其实这个实验除了表现出了小世界现象,还隐藏了一个更深刻的现象。是什么呢?可以想象,每个参加实验的人和股票经纪人之间有多条不同中转路径,有些包含的中间人多,有些包含的中间人少。而这个实验还表明,每个人仅通过局部信息(即他认识的人)做决策,居然把较短的路径给找出来了!!!很多研究人员研究了为什么会这样。作为对比,如果每个人有一个上帝视角知道全局信息,即谁和谁认识每个人都知道,那么很容易找到任何两人之间的最短路径。
我接下来要讲一个跟上面相反的两个问题:
1、假设你在你的微信联系人里面选择一个朋友B,给他发一条消息;B将该消息转发给他自己的一个之前没接收到过该消息的朋友C;依次类推。请问:每个人如何仅用局部信息做决策使得该消息传给更多的人或者说传得更远,或者问每个人仅用局部信息做决策能将该消息传多远?
2、你有没有办法预测,从你这里开始,能把消息传多远,即以你为起点的最长路径有多长?
注意问题1、2并不完全相同,特别地,第2个问题并没有发生实际的传递过程。比如,从你开始,每个人都随机选择一个没有接收过消息的朋友作为下一棒,也许可以把消息传到第100个人小明,而小明的朋友圈所有人都接收过这个消息了,从而传递过程停止。此时,问题1的答案为至少为100;但是,你根本没办法预测出以你为起点的最长路径至少为100那么长,你能确定的预测可能还是长度为1或2。
微信朋友圈其实构成了一个网络结构,上面我提出的问题抽象出来就是:给一个网络,如何仅利用网络局部结构信息搜索出一条尽量长的传播路径(问题1)?如何仅利用局部结构信息预测以一个网络节点为起点的最长路径的长度(问题2)?
据我所了解,除了上面提到的(都比较容易想到的)随机选择方案,之前没有任何其它解决方案。显然研究这两个问题具有重要的理论意义,其应用(大规模商用)意义也许暂时不是很明确。相信迟早会有研究人员进行系统地研究。当然这两个问题应该没有办法一次性给出最优解决方案,只能靠众多研究人员进行大量、长期研究,逐步优化解决方案。
我们利用 [t,p]-chain 分解理论,对这两个问题给出了一个解决方案,大量的计算机仿真评估性能也不错。
最后再讲一个场景。大家在影视剧里面经常看到,情报人员A问情报人员B:“C是不是我们的人?”,B一般回答“我不知道,我也是只跟我接头的人单线联系。”也就是说,对于情报网络,每个人只知道网络的局部信息,这样风险小。如果某种形势下,为了尽可能保存一份重要情报或物件,需要倒腾越多的人越好,怎么办?我们的方案也许能排上用场。