主要研究方向：

1. 对称（置换）群相关的组合数学。代表性成果：

（1）提出平面置换（Plane permutations）新模型，可以作为超地图和地图的新表示方法。通过对平面置换的研究，得到一系列关于超地图和地图的组合计数结果；基于平面置换的相关成果发表在《SIAM Journal on Discrete Mathematics》, 《Advances in Applied Mathematics》,《Journal of Algebraic Combinatorics》,《Discrete Mathematics》等重要期刊上；

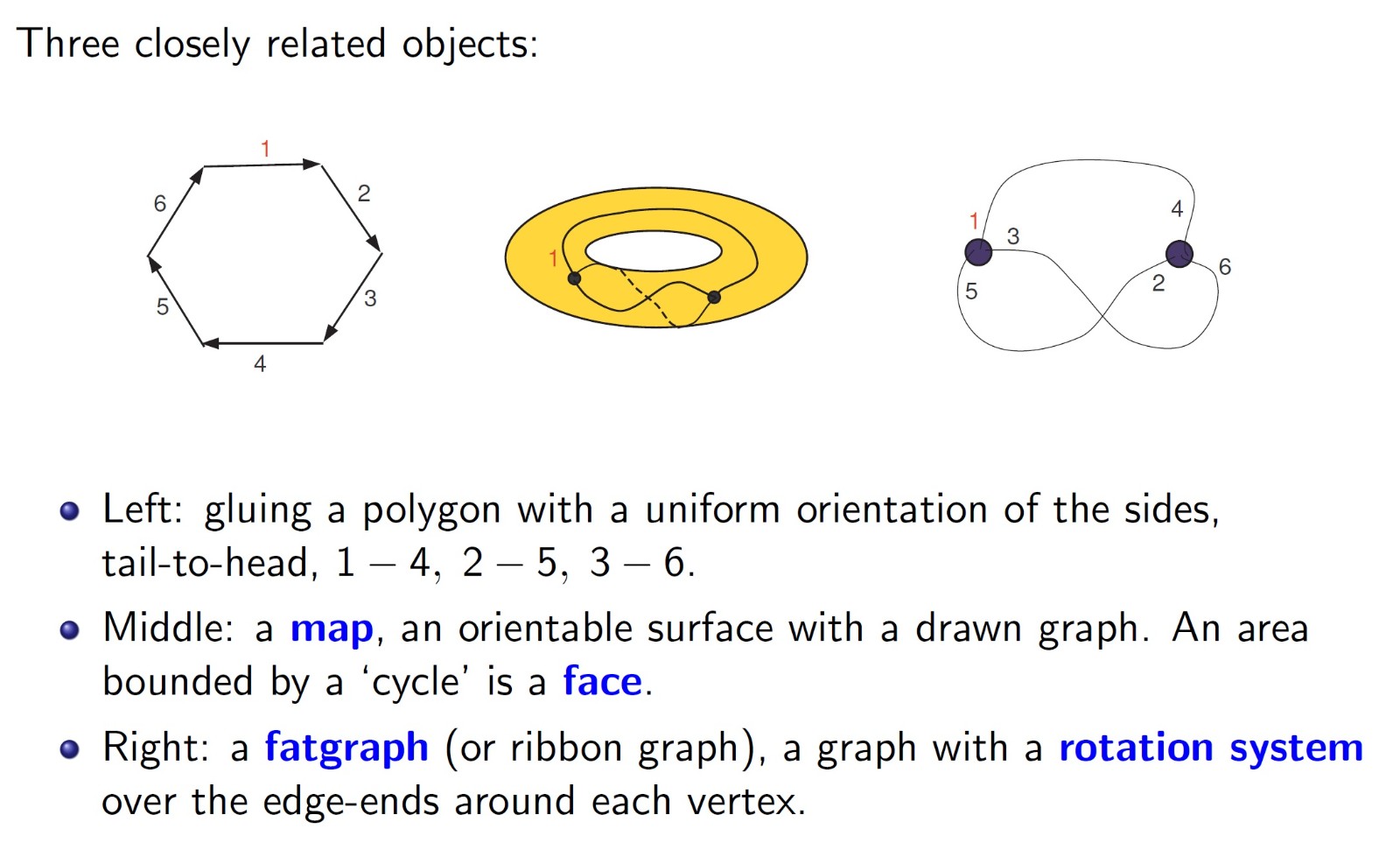
（2）发现并证明了一个广泛成立的置换乘积计数递推公式，从而将著名的 Hurwitz 数计算问题从现有最好结果只能处理两个非单纯分歧点情况推进到处理具有3个非单纯分歧点的情况（称为三重 Hurwitz 数），并应用到地图与超地图的组合计数性质上；相关已发表成果发表在《Journal of Combinatorial Theory Series A》,《Proceedings of American Mathematical Society》等期刊上。

2. 基因序列/RNA/DNA的数学问题研究。代表性成果：

（1）应用平面置换模型，为基因序列对换（transposition）、块交换（block-interchange）和反转（reversal）三种重组操作距离统一地给出了求最大值形式的通用下界，而著名的Bafna-Pevzner下界（引用数上千）为优化范围内一个具体值。该工作发表在《SIAM Journal on Discrete Mathematics》。遗憾的是，求该最大值目前仍然是一个公开问题。

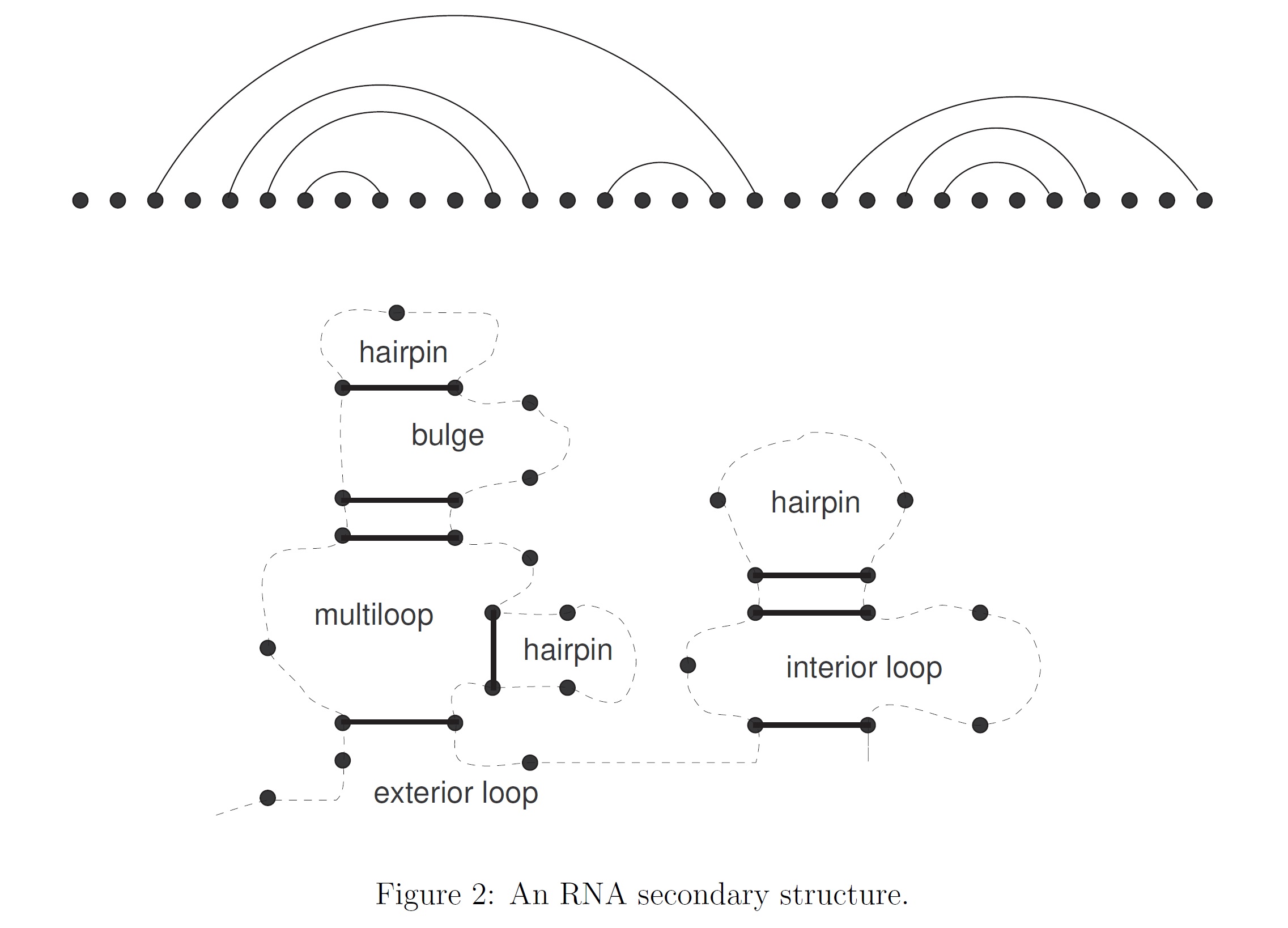
（2）构造了一种平面树与RNA二级结构的新双射对应关系，并发现了平面树横向、纵向分解与奇数层、偶数层的联合同分布性质。相关工作发表在《Electronic Journal of Combinatorics》

（3）提出了平面树的Rake分解，并应用于设计出目前最精细的RNA二级结构随机生成算法。该算法可以随机生成包含任意给定个数和长度的茎区（stack），发夹环（hairpin），凸包（bulge），内环（internal loop），多环（multiloop），外环（exterior loop）的RNA二级结构，编写的 

RakeSamp 软件及其 C 语言代码免费发布在网上（参考论文里网址），供同行免费使用。该工作发表在国际生物数学学会(Society for Mathematical Biology)旗舰期刊《Bulletin of Mathematical Biology》

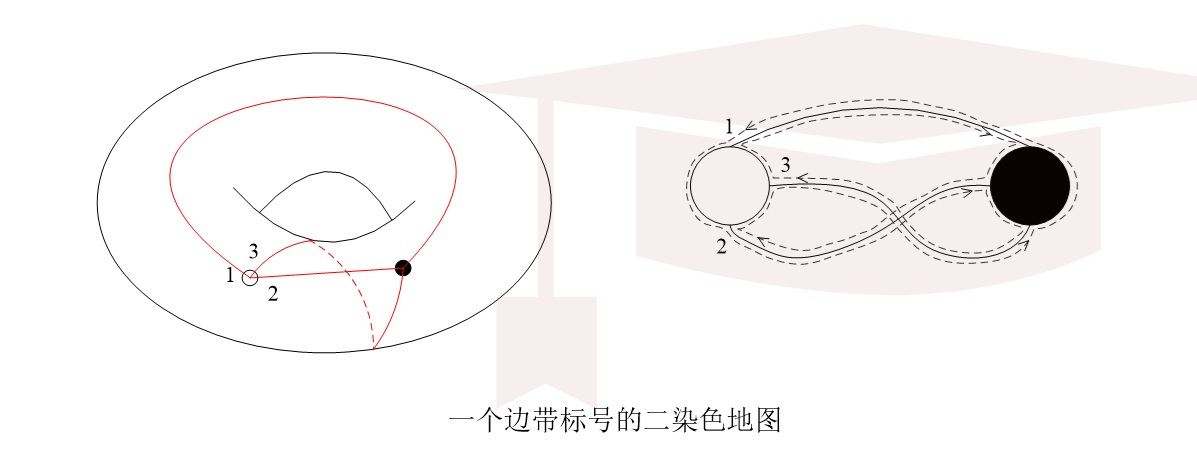
地图和超地图的组合计数问题

一个地图由一个拓扑闭曲面和嵌入其上的图构成，其中要求嵌入形成的每一个面拓扑同胚于一个圆盘。当该拓扑闭曲面可定向且亏格为g时，我们称该地图为一个亏格为g的地图。著名的欧拉示性数公式指出，2-2g=v-e+f，其中v为所嵌入图的顶点个数，e为所嵌入图的边个数，f为形成的面个数。计算（组合计数）满足一些参数条件的不同地图个数是研究地图的一个重要且有难度的问题。超地图是对地图概念的推广，可以理解为把地图的边推广成了更抽象的边类型（而非仅仅是两个顶点之间的连线），相应地有超地图的组合计数问题。等价地，超地图可以转化成顶点二染色的地图，这类地图在代数几何里被著名数学家、菲尔兹奖得主 Grothendieck 称为 dessins d'enfants。超地图和地图的研究跟拓扑学、代数学、自由概率理论与数学物理等领域都有紧密的联系。例如，量子理论里著名的费曼（Feynman）图的计数问题可以转化为地图的计数问题，随机高斯矩阵的研究与地图的组合计数相关。

Hurwitz 问题

著名的 Hurwitz 计数问题是组合计数从一个连通的紧致黎曼曲面X到黎曼（Riemann）球面（有时也讨论更一般的黎曼曲面）的分歧覆盖（ramified or branched covering）的个数（称之为Hurwitz数），由著名数学家赫尔维茨（Hurwitz）一百多年前（1891年）提出。

最基本的Hurwitz问题是计算满足给定分歧点个数和其分歧类型的分歧覆盖个数，其中通常把分歧点区分为单纯分歧点和非单纯分歧点。Hurwitz还将分歧覆盖计算问题转化为了一个等价的代数组合问题，即计算把一个置换分解成其它置换合成的不同分解方案个数。目前有显式计算公式的 Hurwitz 数是关于除单纯分歧点之外具有1个或者2个非单纯分歧点的，具有3个以上非单纯分歧点的没有有效方法计算。

基因序列重组距离问题：

一些生物信息学研究人员观察到两个不同物种的基因序列可能其中一个是另一个经过分段之后的重组。人们也提出了不同的可能的重组方式，我们稍后会介绍其中三种：对换（transposition），块交换（block-interchange）, 反转（reversal）。研究人员认为，一个物种的基因序列经过一定次数的某种重组方式变到另一个物种的基因序列所经过的次数越少，可能反映两个物种在进化意义上比较接近。

基于以上描述的基因序列重组问题，人们研究了如下数字序列重组距离问题。给{1，2，…，n} 这n个数的一个任意序列（排序），如果交换该序列里相邻的两个片段（片段长度不做限制），我们称对该序列做了一次对换；如果不要求两个片段相邻，我们称对该序列做了一次块交换。将该序列通过一系列对换变成12…n（即从小到大的排列）所需要的最少对换次数称之为该序列的对换距离，块交换距离类似定义。块交换距离问题实际上比对换距离问题简单些。

例：假设n=7，给定的序列为 3521764。对换其217和64片段，可得新序列3564217；块交换其52和64片段，可得新序列3641752。

注意到，3521764à3564217à3456217à3456721à2134567à1234567，说明序列3521764的对换距离应该不超过5，具体是多少呢？感兴趣的朋友自己可以动手试一下。

Bafna和Pevzner在1995年SODA会议上提出所谓圈图模型（cycle graph）给出了对换距离的一个下界，该论文目前引用次数近千次。1996年Christie给出了块交换距离的精确计算公式。对换距离至今也没有精确计算公式。

利用我们提出的平面置换（plane permutation）模型，我们把各种距离下界表示成了一个求最大值问题。以对换距离为例，我们的结果如下：

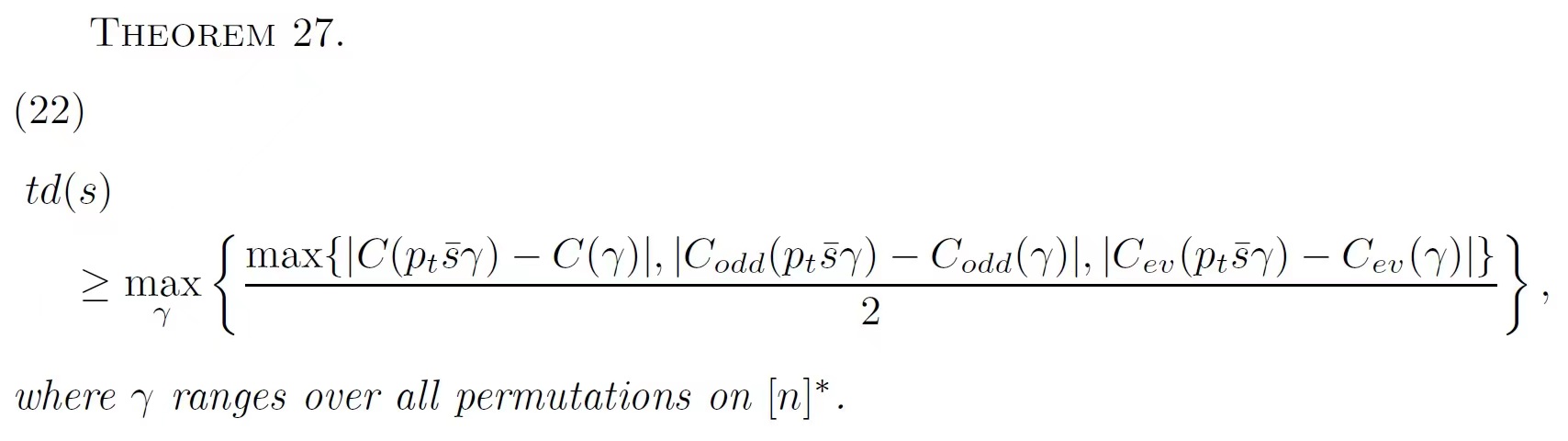
其中，td(s)表示序列s的对换距离，其它公式、符号细节见论文。而上面介绍的Bafna-Pevzner下界仅对应于我们最大值问题优化范围内的某个具体的 gamma 确定的值。显然，我们的下界理论上更好。该结果发表在《SIAM Journal on Discrete Mathematics》期刊上。遗憾的是，我们没能解决该优化问题，求该最大值目前仍然是一个公开问题。

反转就是把一个片段逆序排列。比如，3521764-->3524671。序列的反转距离类似定义。

鲜为人知的是，微软的比尔.盖茨在读书的时候研究过该问题的一个特殊情形，也称之为煎饼排序，即被反转的片段要求只能从序列的首位开始。例：3521764-->1253764-->5213764-->… 比尔.盖茨就此问题发表了一篇论文，他论文里提出的方法目前好像还是最有效的煎饼排序算法